SEGUNDO BGU "A" 2019 - 2020 MATEMATICA

Estimados estudiantes el correo:   ocptareas@gmail.com    👈👀💦está activo para enviar los TRABAJOS  y permanecer comunicados.

Cuídense mucho, saludos.

Ing. Manuel Córdova Mosquera.

MUY IMPORTANTE

Tengo a bien compartir esta información para estar fundamentados en la verdad de los síntomas que debemos tomar en cuenta para reportar a las autoridades de salud. Conviene que conozcamos estas diferencias para no estar alarmados por todo, sino cautos con la verdad de este virus.

MATEMÁTICA SEGUNDO BGU "A"

DESTREZAS CON CRITERIO DE DESEMPEÑO:  

M.5.2.1. Graficar vectores en el plano (coordenadas) identificando sus características: dirección, sentido y longitud o norma.

M.5.2.2. Calcular la longitud o norma (aplicando el teorema de Pitágoras) para establecer la igualdad entre dos vectores.

M.5.2.3. Sumar, restar vectores y multiplicar un escalar por un vector de forma geométrica y de forma analítica, aplicando propiedades de los números reales y de los vectores en el plano.

M.5.2.4. Resolver y plantear problemas de aplicaciones geométricas y físicas (posición, velocidad, aceleración, fuerza, entre otras) de los vectores en el plano, e interpretar y juzgar la validez de las soluciones obtenidas dentro del contexto del problema.

M.5.2.5. Realizar las operaciones de adición entre elementos de R2 y de producto por un número escalar de manera geométrica y analítica aplicando propiedades de los números reales.

M.5.2.6. Reconocer los vectores como elementos geométricos de R2.

M.5.2.7. Calcular el producto escalar entre dos vectores y la norma de un vector para determinar la distancia entre dos puntos A y B en R2 como la norma del vector.

M.5.2.8. Reconocer que dos vectores son ortogonales cuando su producto escalar es cero, y aplicar el teorema de Pitágoras para resolver y plantear aplicaciones geométricas con operaciones y elementos de R2, apoyándose en el uso de las TIC (software como Geogebra, calculadora gráfica, applets en Internet).

M.5.2.9. Escribir y reconocer la ecuación vectorial y paramétrica de una recta a partir de un punto de la recta y un vector dirección, o a partir de dos puntos de la recta.

M.5.2.10. Identificar la pendiente de una recta a partir de la ecuación vectorial de la recta, para escribir la ecuación cartesiana de la recta y la ecuación general de la recta.

M.5.2.11. Determinar la posición relativa de dos rectas en R2 (rectas paralelas, que se cortan, perpendiculares) en la resolución de problemas (por ejemplo: trayectoria de aviones o de barcos para determinar si se interceptan).

M.5.2.12. Calcular la distancia de un punto P a una recta (como la longitud del vector formado por el punto P y la proyección perpendicular del punto en la recta P´, utilizando la condición de ortogonalidad del vector dirección de la recta y el vector) en la resolución de problemas (distancia entre dos rectas paralelas).

M.5.2.13. Determinar la ecuación de la recta bisectriz de un ángulo como aplicación de la distancia de un punto a una recta.

M.5.2.14. Resolver y plantear aplicaciones de la ecuación vectorial, paramétrica y cartesiana de la recta con apoyo de las TIC.

M.5.2.15. Aplicar el producto escalar entre dos vectores, la norma de un vector, la distancia entre dos puntos, el ángulo entre dos vectores y la proyección ortogonal de un vector sobre otro, para resolver problemas geométricos, reales o hipotéticos, en R2.

CLASE N° 41                        FECHA: 16 de marzo de 2020

TEMA: DISTANCIA ENTRE DOS PUNTOS

Pagina # 137
TAREA N° 1: Elaborar un resumen en el cuaderno Anexo # 1
 ( Abrir este enlace con un Clic ) ⟸👀

Ejercicio # 1
Calcular el Perímetro de un triángulo cuyas coordenadas de sus vértices son:

A(5, 1)              B(–3,  –5)             C(–3, 7)

                                                      Fórmula de la distancia:  d = √(X₂ – X₁)² + (Y₂ – Y₁)²

PROCEDIMIENTO:

1)      Representar gráficamente las coordenadas en el plano cartesiano y dibujar el triángulo ABC

2)      Calcular mediante la fórmula de la distancia; la longitud de sus lados:

        Respuesta: AB= 10cm, AC=10cm, BC= 12cm

3)      Sumar los valores encontrados y hallar el perímetro.
        Respuesta: perímetro P=32cm.

㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔

CLASE N° 42                        FECHA: 17 de marzo de 2020

TEMA: ANGULO ENTRE VECTORES en R2.

Pagina # 137 - 138
TAREA N° 2: Ejercicio # 2  y Elaborar un resumen en el cuaderno
 (Clic para abrir el archivo ) ⟸👀

Calcular los ángulos interiores de un triángulo cuyas coordenadas de sus vértices son:

A(–2, –1)              B(2,  –5)             C(4, 1)

PROCEDIMIENTO:

1)      Representar gráficamente las coordenadas en el plano cartesiano y dibujar el triángulo ABC

2)      Calcular mediante la fórmula de la distancia la longitud de sus lados:

Respuesta: AB=𒑟32; BC=𒑟40; AC=𒑟40

3)      Calcular el producto escalar de sus lados adyacentes:

Respuesta: AB – BC = 16; AB – AC = 16; AC – BC = 24

4)      Calcular los ángulos interiores mediante la fórmula:

Respuesta: α = 63°26´5,82”     β = 63°26´5,82”     ϕ = 53°7´48,37”

NOTA: Es un triángulo Isósceles porque tiene dos lados y dos ángulos iguales.

㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔

CLASE N° 43                        FECHA: 20 de marzo de 2020

TEMA: DISTANCIA ENTRE DOS PUNTOS

Página # 137 - 138

TAREA N° 3: Desarrollar el Ejercicio # 3 

Demostrar que la figura delimitada por las coordenadas:

A(– 4, 6); B(2, – 2); C(–2, –5) y D(–8, 3) es un Rectángulo

Definición. Rectángulo es un cuadrilátero cuyos dos lados opuestos son iguales y todos los cuatro ángulos son iguales también

Condiciones para que una figura geométrica sea un Rectángulo:

1. Los lados opuestos de un rectángulo tienen la misma longitud, o sea, son iguales:

AB = CD,   BC = AD

2. Los lados opuestos de un rectángulo son paralelos:

AB||CD,   BC||AD

3. Los lados adyacentes de un rectángulo siempre son perpendiculares:

AB _┴ BC,   BC _┴ CD,   CD _┴ AD,   AD _┴ AB

4. Todos los cuatro ángulos de un rectángulo son rectos:

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°

5. La suma de los ángulos de un rectángulo es igual a 360°:

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

6. Las diagonales de un rectángulo tienen las longitudes iguales:

AC = BD

7. La suma de los cuadrados de las diagonales de un rectángulo es igual a la suma de los cuadrados de los lados:

2d² = 2a² + 2b²

PROCEDIMIENTO:

Graficar la figura en el plano cartesiano asignado las coordenadas de los vértices.

Primera condición: Los lados opuestos de un rectángulo tienen la misma longitud, o sea, son iguales:       AB = CD;   BC = AD

1)      Debemos calcular la distancia entre dos puntos y hallar la longitud de los lados mediante la fórmula:    d = √(X₂ – X₁)² + (Y₂ – Y₁)²

2)      En donde: AB = 10,          BC = 5,            CD = 10,         AD = 5

3)      Demostramos por lo tanto que los lados opuestos son iguales: AB = CD;   BC = AD

Segunda condición: Los lados opuestos de un rectángulo son paralelos:  AB||CD,   BC||AD

 

1)      Debemos aplicar la condición de paralelismo: Página # 133    AxBy = AyBx

2)      Determinamos las coordenadas vectoriales de AB(– 6i, 8j) y CD(– 6i, 8j)

3)      Aplicamos la fórmula y demostramos que los lados son paralelos.

㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔

CLASE N° 44                        FECHA: 23 de marzo de 2020

TEMA: DISTANCIA ENTRE DOS PUNTOS

Página # 137 - 138

TAREA N° 4: Desarrollar el Ejercicio # 3

(continuación)

Tercera condición: Los lados adyacentes de un rectángulo siempre son perpendiculares:

 A* B = 0AB _┴ BC,        BC _┴ CD,        CD _┴ AD,       AD _┴ AB

1)      Debemos aplicar la condición de paralelismo: Página # 132  

2)      Determinamos las coordenadas vectoriales de AD(4i, 3j) y BC(4i, 3j)

3)      Aplicamos la fórmula multiplicando: AB * BC y CD * AD

4)      Demostramos que los lados son perpendiculares.

Cuarta condición: Todos los cuatro ángulos de un rectángulo son rectos:

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°

Esta condición ya fue demostrada por que los lados perpendiculares forman un ángulo de 90°

Quinta condición: La suma de los ángulos de un rectángulo es igual a 360°:

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

Igualmente, ya demostrada.

㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔

CLASE N° 45                        FECHA: 24 de marzo de 2020

TEMA: DISTANCIA ENTRE DOS PUNTOS

Página # 137 - 138

TAREA N° 5: Desarrollar el Ejercicio # 3 

(continuación)

Sexta condición: Las diagonales de un rectángulo tienen las longitudes iguales: 
AC = BD

1)      Debemos calcular la distancia entre dos puntos y hallar la longitud de las Diagonales mediante la fórmula:   d = √(X₂ – X₁)² + (Y₂ – Y₁)²

2)   En donde: AC = 5√5,       BD =5√5

3)      Demostramos por lo tanto que las Diagonales son iguales: AC = BD

_______________________________________________________________________

Séptima condición: La suma de los cuadrados de las diagonales de un rectángulo es igual a la suma de los cuadrados de los lados: 2d² = 2a² + 2b²

Diagonal = 5√5

Lado mayor = 10        valores ya determinados anteriormente.

Lado menor = 5

Aplicamos la Relación: 2d² = 2a² + 2b²   y demostramos que 250 = 250

REPRESENTACIÓN GRÁFICA

Fin ejercicio # 3

㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔

CLASE N° 46                        FECHA: 27 de marzo de 2020

TEMA: DISTANCIA ENTRE DOS PUNTOS

Página # 137 - 138

TAREA N° 6: Desarrollar el Ejercicio # 4 

Demostrar que la figura delimitada por las coordenadas:

 A(3, 6); B(8, –6); C(–4, –1) y D(–9, 11) es un Rombo y Calcular su Perímetro y Área.

Condiciones para que una figura geométrica sea un Rombo:

1)      Sus dos lados adyacentes son iguales (de esto se deduce que todos los lados son iguales): 

       AB = BC = CD = AD

2)      Sus lados no adyacentes son paralelos:  AB // CD y AD // BC

3)      Sus diagonales son segmentos perpendiculares que unen los vértices no consecutivos.

AC┴BD

4)      Sus cuatro ángulos interiores (dos α y dos β) son iguales dos a dos.

PROCEDIMIENTO:

1)      Dibujar la figura en el plano cartesiano

Primera condición: Sus dos lados adyacentes son iguales (de esto se deduce que todos los lados son iguales): AB = BC = CD = AD

1)      Debemos calcular la distancia entre dos puntos y hallar la longitud de los lados mediante la fórmula:    d = √(X₂ – X₁)² + (Y₂ – Y₁)²

2)      En donde: AB = 13,          BC = 13,          CD = 13,         AD = 13

3)      Demostramos por lo tanto que sus lados son iguales: AB = BC = CD = AD

Segunda condición: Sus lados no adyacentes son paralelos:  AB // CD y AD // BC

1)      Debemos aplicar la condición de paralelismo: Página # 133  AxBy = AyBx

2)      Determinamos las coordenadas vectoriales de AB(– 5i, 12j) y CD(– 5i, 12j)

3)      Aplicamos la fórmula y demostramos que los lados son paralelos: AB // CD

4)      Determinamos las coordenadas vectoriales de AD(– 12i, 5j) y BC(– 12i, 5j)

5)      Aplicamos la fórmula y demostramos que los lados son paralelos: AD // BC

㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔

CLASE N° 47                        FECHA: 30 de marzo de 2020

TEMA: DISTANCIA ENTRE DOS PUNTOS

Página # 137 - 138

TAREA N° 7: Desarrollar el Ejercicio # 4 

(continuación)

Tercera condición: Sus diagonales son segmentos perpendiculares que unen los vértices no consecutivos.  AC┴BD

 

1)      Debemos aplicar la condición de paralelismo: Página # 132    A * B = 0

2)      Determinamos las coordenadas vectoriales de:

Diagonal menor AC(7i, 7j)

Diagonal mayor BD(–17i, 17j)

3)      Aplicamos la fórmula multiplicando: AC por BD

4)      Demostramos que los lados son perpendiculares.

Como también se pide Calcular el perímetro y el área:

PERIMETRO:

El perímetro es la suma de los lados, por lo tanto, P = AB + BC + CD + AD

Valores de los lados que ya tenemos calculados: P = 13+13+13+13, P = 48

AREA:

Para encontrar el área tenemos que aplicar la fórmula:  A = (D*d) / 2

1)     
Debemos calcular la longitud de las diagonales aplicando la fórmula para la distancia entre dos puntos:

2)      En donde:

d  ⇒    Diagonal menor    AC = √98

D ⇒    Diagonal mayor    BD = √578

3)      Aplicamos la fórmula de área y obtenemos A = 119

㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔

CLASE N° 48                        FECHA: 31 de marzo de 2020

TEMA: DISTANCIA ENTRE DOS PUNTOS

Página # 137 - 138

TAREA N° 8: Desarrollar el Ejercicio # 4 

(continuación)

Cuarta condición: Sus cuatro ángulos interiores (dos α y dos β) son iguales dos a dos.

Calcular el producto escalar de sus lados adyacentes:

RESPUESTA:  AB – BC = 120

BC – CD = –120

Calcular los valores modulares = 13

Calcular los ángulos interiores mediante la fórmula:

RESPUESTA: α = 135°14´23.0”     β = 44°45´36,97”

      Por lo tanto 2 α + 2 β = 360°

㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔

CLASE N° 49                        FECHA: 03 de abril de 2020

TEMA: 2. ECUACIONES DE LA RECTA

2.1 ECUACIÓN CARTESIANA DE LA RECTA (Forma Explícita)

Página # 140

TAREA N° 9: Pasar la materia al cuaderno 👈😉Clic aquí

La materia se encuentra en el enlace.

㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔

CLASE N° 50                        FECHA: 06 de abril de 2020

TEMA: 2. ECUACIONES DE LA RECTA

2.1 ECUACIÓN CARTESIANA DE LA RECTA (Forma Explícita)

Página # 140

TAREA N° 10: Resolver el Ejercicio # 5

Hallar la Ecuación Cartesiana de la Recta que pasa por los puntos:

1.      E(– 2, 3) y F(– 5, – 6)             RESPUESTA:    y =  3 x + 9

2.      H(3, – 1) y K(– 2, 9)               RESPUESTA:    y = – 2 x + 5

Representar cada Ecuación en un plano cartesiano.

㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔

CLASE N° 51                        FECHA: 07 de abril de 2020

TEMA: 2. ECUACIONES DE LA RECTA

2.1 ECUACIÓN CARTESIANA DE LA RECTA (Forma Explícita)

Página # 140

TAREA N° 11: Resolver el Ejercicio # 6

Hallar la Ecuación Cartesiana de la Recta que pasa por los puntos:

1.      R(– 6, 2) y S(1, – 5)                RESPUESTA:    y =  – x –  4

2.      T(4, – 3) y U(– 2, – 6)            RESPUESTA:    y =  1/2 x – 5

Representar cada Ecuación en un plano cartesiano.

㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔

CLASE N° 52                        FECHA: 13 de abril de 2020

TEMA:  ECUACIÓN DE UNA RECTA PARALELA A UNA RECTA CONOCIDA

Página # 147   👈😉Clic aquí

TAREA N° 12:          Pasar la materia al cuaderno       VER VIDEO

Resolver el Ejercicio # 7

Ejercicio # 7

Hallar la Ecuación de la Recta que pasa por los puntos (2, 3) y es paralela a la recta:

y = 4x – 2    Dibuja la gráfica con las dos rectas.

Hallar la Ecuación de la Recta que pasa por los puntos (1, 2) y es paralela a la recta:

y = – 2x + 5             Dibuja la gráfica con las dos rectas.

㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔

CLASE N° 53                        FECHA: 14 de abril de 2020

TEMA:  ECUACIÓN DE UNA RECTA PERPENDICULAR A UNA RECTA CONOCIDA

Página # 148  👈😉Clic aquí

TAREA N° 13:          Pasar la materia al cuaderno   VER VIDEO

Resolver el Ejercicio # 8

Ejercicio # 8

Hallar la Ecuación de la Recta que pasa por los puntos (4, 2) y es perpendicular a la recta:

y = 2x – 1    Dibuja la gráfica con las dos rectas.

Hallar la Ecuación de la Recta que pasa por los puntos (1, 3) y es perpendicular a la recta:

y = – x + 4   Dibuja la gráfica con las dos rectas.

㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔

㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔

CLASE N° 54                        FECHA: 17 de abril de 2020

TEMA:           PRUEBA DE BLOQUE N° 4  👈😷💥Clic aquí

DESARROLLAR LA PRUEBA EN EL CUADERNO

㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔

UNIDAD N° 5

Texto de Matemática 2° BGU: https://educacion.gob.ec/libros-de-texto/

CLASE N° 55                                                FECHA: 27 de abril de 2020

TEMA:           ESTADISTICA

Página #196👈Clic aquí💥

TAREA N° 1: Realizar en el cuaderno un resumen de la página 196

                        Desarrollar el ejercicio N° 1

DESTREZAS CON CRITERIO DE DESEMPEÑO A DESARROLLAR:      (Informativo)

M.4.3.1. Organizar datos procesados en tablas de frecuencias para definir la función asociada y representarlos gráficamente con ayuda de las TIC.

M.4.3.2. Organizar datos (edades, estaturas, precios de productos, etc.) no agrupados (máximo 20) y datos agrupados (máximo 50) en tablas de distribución de frecuencias: absoluta, relativa, relativa acumulada y acumulada para analizar el significado de los datos para una compresión mayor de la información encontrada en varios medios.

M.4.3.3. Representar de manera gráfica, con el uso de la tecnología, las frecuencias: histograma o gráfico con barras (polígono de frecuencias), gráfico de frecuencias acumuladas (ojiva), diagrama circular en función de analizar datos mejorando la capacidad de compresión de la información presentada de forma gráfica por los medios de comunicación.

M.5.3.2. Resolver y plantear problemas de aplicación de las medidas de tendencia central y de dispersión para datos agrupados, con apoyo de las TIC.

M.5.3.3. Juzgar la validez de las soluciones obtenidas en los problemas de aplicación de las medidas de tendencia central y de dispersión para datos agrupados dentro del contexto del problema, con apoyo de las TIC.

M.5.3.4. Calcular e interpretar el coeficiente de variación de un conjunto de datos (agrupados y no agrupados).

La Estadística

Población y muestra

Población

Muestra

Las variables y sus tipos

Ejercicio N° 1

Indica cuál es la población y la variable estadística de cada uno de los siguientes estudios esdísticos. Señala, además, de qué tipo es la variable estadística.

a.  Preferencias deportivas de los alumnos de tu clase.

b.  Tiempo medio invertido por los trabajadores españoles en desplazarse desde su domicilio hasta el centro de trabajo.

c.  Número de veces, en un año, que asisten al teatro los habitantes de tu localidad.

㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔

CLASE N° 56                                                FECHA: 28 de abril de 2020

TEMA:           ESTADISTICA

Página # 197👈Clic aquí💥

TAREA N° 2: Realizar en el cuaderno un resumen de la página 197

                        Desarrollar el ejercicios N° 2

Las variables y sus tipos

Cuadro sinóptico de las Variables Estadísticas

1.1. La recolección de datos y su interpretación

Ejercicio N° 2

 Se realiza un estudio para determinar el grado de satisfacción del nivel educativo

en el Colegio Octavio Cordero Palacios, que encuestó a 100 estudiantes de los cursos

de bachillerato.

a)      Identifica la población, muestra, variable y tipo de variable

b)      Clasifica las siguientes variables en cualitativas o cuantitativas: Edad, ocupación, nacionalidad, remuneración económica, hijos, signo zodiacal, comida preferida.

c)      Escribe tres ejemplos de variables cualitativas nominales y ordinales.

d)      Describe tres ejemplos de variables cuantitativa.

㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔㆔

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

CLASE N° 57                                                FECHA: 04 de Mayo de 2020

TEMA: 1.2. TABLA DE FRECUENCIA PARA DATOS NO AGRUPADOS

Página # 198

TAREA N° 3: Realizar en el cuaderno un resumen de la página 198

                         

1.2. Tabla de frecuencia para datos no agrupados

FECHA DE ENTREGA: Domingo 10 de mayo 2020 hasta las 22:00 horas

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

CLASE N° 58                                                FECHA: 05 de mayo de 2020

TEMA: 1.3. PRESENTACIÓN DE INFORMACIÓN

Página # 198

TAREA N° 4: Pasar al cuaderno la materia

                         

DISTRIBUCIÓN DE TABLAS DE FRECUENCIAS

Estadística Descriptiva:

Tienen por objeto fundamental describir y analizar las características de un conjunto de datos, obteniéndose de esa manera conclusiones sobre las características de dicho conjunto y sobre las relaciones existentes con otras poblaciones, a fin de compararlas. No obstante, puede no solo referirse a la observación de todos los elementos de una población (observación exhaustiva) sino también a la descripción de los elementos de una muestra (observación parcial).

En relación a la estadística descriptiva, Ernesto Rivas Gonzáles dice; "Para el estudio de estas muestras, la estadística descriptiva nos provee de todos sus medidas; medidas que cuando quieran ser aplicadas al universo total, no tendrán la misma exactitud que tienen para la muestra, es decir al estimarse para el universo vendrá dada con cierto margen de error; esto significa que el valor de la medida calculada para la muestra, en el oscilará dentro de cierto límite de confianza, que casi siempre es de un 95 a 99% de los casos.

Distribución de frecuencias: muestra el número de veces que ocurre cada observación.

Ejemplo: Se elaboró una encuesta en un jardín de niños y ésta informó que las mascotas más comunes que tiene un niño son perros, gatos, peces, hámsteres y pájaros

perro	gato	perro	hámster	hámster	gato	pájaro	gato	perro	perro
pájaro	hámster	gato	perro	perro	perro	hámster	pájaro	pájaro	gato

 A continuación, se muestra la distribución de frecuencias absolutas, relativas y porcentuales de las mascotas más comunes de los niños.

Mascota	Frecuencia absoluta	Frecuencia relativa	Frecuencia acumulada
Perro	7	0.35 – 35%	7
Pájaro	4	0.20 – 20%	11
Hámster	4	0.20 – 20%	15
Gato	5	0.25 – 25%	20
TOTAL    =	20	1,00 – 100%

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

CLASE N° 59                                     FECHA: 08 de mayo de 2020

TEMA: TABLA DE FRECUENCIAS DE DATOS ESTADÍSTICOS

TAREA N° 5: Transcribir al cuaderno, un ejemplo  .... Ver los Vídeos:

VIDEO # 1           

https://www.youtube.com/watch?time_continue=13&v=a7DWGLpdIuI&feature=emb_logo

VIDEO # 2
https://www.youtube.com/watch?time_continue=12&v=cyXenZEbGz4&feature=emb_logo

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

CLASE N° 60                                    FECHA: 11 de mayo de 2020

TEMA: REPRESENTACION GRAFICA DE DATOS ESTADÍSTICOS

TAREA N° 6: Transcribir al cuaderno (Imprimir y pegar)

Las tablas de frecuencias se representan generalmente acompañadas de gráficos estadísticos para permitir una mayor y mejor visualización de los datos.

VER VIDEO:  👇👀           

https://www.youtube.com/watch?v=Mfpb1BtT_10&feature=emb_logo

NOTA: Los estudiantes que no tengan computadora hagan los gráficos manualmente (solo el de barras)

CLASE N° 61                                    FECHA: 12 de mayo de 2020

TEMA: TABLA DE FRECUENCIAS Y GRAFICO ESTADÍSTICO

TAREA N° 7: Resolver el ejercicio del CASO # 1

CASO # 1

Se ha realizado una encuesta a 31 estudiantes del Segundo año de BGU de la Unidad Educativa "Octavio Cordero Palacios" de la Ciudad de Cuenca, sobre el número de horas que utilizan Internet en el día. Las respuestas obtenidas fueron:

NUMERO DE HORAS:

1	2	3	4	2	3	2
5	1	2	3	4	6
4	2	1	2	3	5
7	3	2	1	2	6
2	4	3	2	1	5

Se pide.

1)      Realizar el conteo de datos.

2)      Elaborar una Tabla de Distribución de Frecuencias

3)      Diseñar un Gráfico Estadístico apropiado. (barras, pastel)

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

CLASE N° 62                                    FECHA: 15 de mayo de 2020

TEMA: TABLA DE FRECUENCIAS Y GRÁFICO ESTADÍSTICO

TAREA N° 8: Resolver el ejercicio del CASO # 2

CASO # 2

Se ha realizado una encuesta a 24 estudiantes del Segundo año de BGU de la Unidad Educativa "Octavio Cordero Palacios" de la Ciudad de Cuenca, sobre su lugar de nacimiento. Las respuestas obtenidas fueron:

LUGAR DE NACIMIENTO:

San Joaquín	El Valle	Ricaurte	Sayausi	Quinta Chica	Ricaurte
Sayausi	Sayausi	Quinta Chica	Ricaurte	San Joaquín	El Valle
El Valle	Ricaurte	San Joaquín	Quinta Chica	Ricaurte	Sayausi
Ricaurte	Quinta Chica	Sayausi	Ricaurte	Sayausi	Ricaurte

Se pide.

1)      Realizar el conteo de datos.

2)      Elaborar una Tabla de Distribución de Frecuencias

3)      Diseñar un Gráfico Estadístico apropiado. (barras, pastel)

NOTA:  Los alumnos que no pueda utilizar Excel ... 

Elaboren manualmente un gráfico de barras

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

CLASE N° 63                                    FECHA: 26 de mayo de 2020

TEMA: CONCLUSIONES DE UN ESTUDIO ESTADÍSTICO

TAREA N° 9: Pasar al cuaderno las Conclusiones

 Resolver el ejercicio del CASO # 3

FECHA DE ENTREGA: Domingo 31 de mayo 2020 hasta las 22:00 horas

CONCLUSIONES

Una conclusión del trabajo de investigación se produce cuando a partir de hechos conocidos se obtiene un nuevo conocimiento.

Es la parte final del proceso investigativo, consiste en elaborar un resume de los argumentos con el propósito de comunicar información de los resultados obtenidos de la investigación, o el análisis sobre un tema

Caso 1:

·         La mayoría de estudiantes (10) utilizan 2 horas diarias de Internet

Caso 2:

·         La mayoría de estudiantes (8) han nacido en Ricaurte.

CASO # 3 Se ha realizado una encuesta a 36 estudiantes del Segundo año de BGU de la Unidad Educativa "Octavio Cordero Palacios" de la Ciudad de Cuenca, sobre su EDAD en años cumplidos hasta la fecha. Las respuestas obtenidas fueron:

EDAD:

18	20	24	26	20	24	29	20	24
20	18	20	22	24	31	20	24	29
22	24	18	20	29	20	24	29	26
24	20	31	18	20	24	20	26	20

Se pide.

1)      Realizar el conteo de datos.

2)      Elaborar una Tabla de Distribución de Frecuencias

3)      Diseñar un Gráfico Estadístico apropiado. (barras, pastel)

4)      Redactar Conclusiones

NOTA:  Los alumnos que no pueda utilizar Excel ... 

Elaboren manualmente un gráfico de barras

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

CLASE N° 64                                    FECHA: 29 de mayo de 2020

TEMA:           MEDIDAS DE TENDENCIA CENTRAL

TAREA N° 10:        Pasar la materia al cuaderno
                               Archivo adjunto 👈👀💦 hacer clic aquí

                             Ver el Video y hacer un resumen 👇💥

https://www.youtube.com/watch?time_continue=8&v=0DA7Wtz1ddg&feature=emb_logo

FECHA DE ENTREGA: Domingo 07 de junio 2020 hasta las 22:00 horas

Las medidas de tendencia central son medidas estadísticas que pretenden resumir en un solo valor a un conjunto de valores. Representan un centro en torno al cual se encuentra ubicado el conjunto de los datos. Las medidas de tendencia central más utilizadas son: media, mediana y moda

Las medidas de tendencia central solamente son aplicables a variables cuantitativas💣💥
Media Aritmética
Mediana
Moda

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

CLASE N° 65                                    FECHA: 01 de junio de 2020

TEMA:           CORRECCION

TAREA N° 11: Realizar la corrección del caso 1 y 2

FECHA DE ENTREGA: Domingo 07 de junio 2020 hasta las 22:00 horas

CORRECCION: CASO # 1  Compare y realice las correcciones necesarias

NUMERO DE HORAS DE INTERNET

HORAS	Frecuencia absoluta	Frecuencia relativa		Frecuencia acumulada
		Valor	%
1h	5	0,16	16%	5
2h	10	0,32	32%	15
3h	6	0,19	19%	21
4h	4	0,13	13%	25
5h	3	0,10	10%	28
6h	2	0,06	6%	30
7h	1	0,03	3%	31
SUMA =	31	1	100%

⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗

CORRECCION: CASO # 2  Compare y realice las correcciones necesarias

LUGAR DE NACIMIENTO

Lugar	Frecuencia absoluta	Frecuencia relativa		Frecuencia acumulada
		Valor	%
San Joaquín	3	0,13	13%	3
Sayausi	6	0,25	25%	9
El Valle	3	0,13	13%	12
Ricaurte	8	0,32	32%	20
Quinta Chica	4	0,17	17%	24
SUMA =	24	1	100%

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶ 

CLASE N° 66                                    FECHA: 02 de junio de 2020

TEMA:           MEDIDAS DE TENDENCIA CENTRAL

TAREA N° 12: Aplicar las medidas de tendencia central al CASO # 3 

FECHA DE ENTREGA: Domingo 07 de junio 2020 hasta las 22:00 horas

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

CLASE N° 67                                    FECHA: 05 de junio de 2020

TEMA:           MEDIDAS DE TENDENCIA CENTRAL

TAREA N° 13: Aplicar las medidas de tendencia central al CASO # 1 

FECHA DE ENTREGA: Domingo 07 de junio 2020 hasta las 22:00 horas

⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗⤗

CORRECCIÓN: Compare con su trabajo y realice las correcciones requeridas

TABLA DE FRECUENCIAS
EDAD DE LOS ESTUDIANTES   CASO # 3

Edad	Frecuencia absoluta	Frecuencia relativa		Frecuencia acumulada
		Valor	%
18	4	0,11	11%	4
20	12	0,33	33%	16
22	2	0,06	6%	18
24	9	0,25	25%	27
26	3	0,08	8%	30
29	4	0,11	11%	34
31	2	0,06	6%	36
SUMA	36	1	100%

REPRESENTACION GRAFICA

Conclusiones: ______________________________________________

Medidas de tendencia central   CASO # 3

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

CLASE N° 68                                    FECHA: 08 de junio de 2020

TEMA:           MEDIDAS DE TENDENCIA CENTRAL

TAREA N° 14: Aplicar las medidas de tendencia central al CASO # 4 

FECHA DE ENTREGA: Domingo 14 de junio 2020 hasta las 22:00 horas

CASO # 4       Se ha realizado una encuesta a los trabajadores de una fábrica de alimentos en la ciudad de Cuenca sobre su peso en kilogramos, obteniendo los siguientes resultados:

53        56        65        73        65

60        53        56        65        74

63        60        53        56        68

65        73        60        53        73

68        65        73        60        65

Se pide:

1)      Realizar el conteo de datos.

2)      Elaborar una Tabla de Distribución de Frecuencias

3)      Diseñar un Gráfico Estadístico apropiado. (barras, pastel)

4)      Hallar las Medidas de Tendencia Central

5)      Redactar conclusiones

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

CLASE N° 69                                    FECHA: 09 de junio de 2020

TEMA:           MEDIDAS DE TENDENCIA CENTRAL

TAREA N° 15: Plantee y resuelva su propio ejercicio estadístico CASO # 5

1)      Realizar el conteo de datos.

2)      Elaborar una Tabla de Distribución de Frecuencias

3)      Diseñar un Gráfico Estadístico apropiado. (barras o pastel)

4)      Hallar las Medidas de Tendencia Central

5)      Redactar conclusiones

FECHA DE ENTREGA: Domingo 14 de junio 2020 hasta las 22:00 horas

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

CLASE N° 70                                    FECHA: 12 de junio de 2020

TEMA:           prueba de bloque n° 5

FECHA DE ENTREGA: Domingo 14 de junio 2020 hasta las 22:00 horas

💥💥💥💥💥💥💥💥💥💥💥💥💥💥💥💥💥💥💥💥💥💥💥
⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

UNIDAD N° 6

CLASE N° 71                                                FECHA: 15 de junio de 2020

TEMA:           CONICAS

Página # 162

TAREA N° 1: Realizar en el cuaderno un resumen de la página 162

DESTREZAS CON CRITERIO DE DESEMPEÑO A DESARROLLAR:      (Informativo)

M.5.2.16. Describir la circunferencia, la parábola, la elipse y la hipérbola como lugares geométricos en el plano. M.5.2.17. Escribir y reconocer las ecuaciones cartesianas de la circunferencia,

la parábola, la elipse y la hipérbola con centro en el origen y con centro fuera del origen para resolver y plantear problemas (por ejemplo, en física: órbitas planetarias, tiro parabólico, etc.),  identificando la validez y pertinencia de los resultados obtenidos.

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

CLASE N° 72                                                FECHA: 16 de junio de 2020

TEMA:           CONICAS

Página # 162

TAREA N° 2: Realizar en el cuaderno un resumen de la página 162

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

CLASE N° 73                                                FECHA: 19 de junio de 2020

TEMA:           CONICAS

Página # 163

TAREA N° 3: Realizar en el cuaderno un resumen de la página 163

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

CLASE N° 74                                                FECHA: 22 de junio de 2020

TEMA:           CONICAS

Página # 165

TAREA N° 4: Realizar en el cuaderno un resumen de la página 165

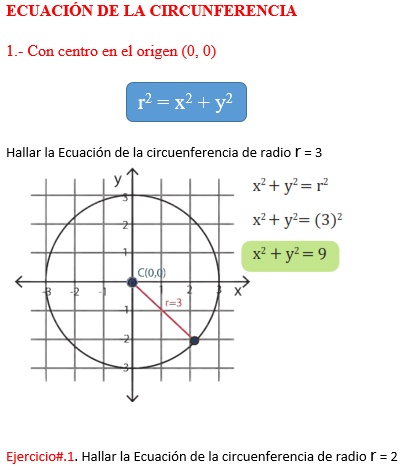
ECUACIÓN DE LA CIRCUNFERENCIA

2.- Con centro en (h, k)

Ejercicio Modelo:

Ejercicio # 2.

Hallar la ecuación de la circunferencia

con centro en el punto P (– 4, 5) y radio 3

Elaborar el gráfico.

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

CLASE N° 75                                                FECHA: 23 de junio de 2020

TEMA:           CONICAS

Página # 165

TAREA N° 5: Plantear y resolver un ejercicio propio.

ECUACIÓN DE LA CIRCUNFERENCIA

2.- Con centro en (h, k)

Ejercicio # 3.

Hallar la Ecuación de la Circunferencia

con centro en el punto M ( ……) y radio …..

Elaborar el gráfico.

Nota: El punto M. está en cualquier cuadrante del plano cartesiano.

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶
CLASE N° 76                                                FECHA: 26 de junio de 2020

TEMA:           CARATULA Y RUBRICA👈👀💦

 Modelo de Caratula para el portafolio estudiantil

Solo llenar el recuadro (PARTICIPACIÓN)

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

CLASE N° 77                                                FECHA: 29 de junio de 2020

TEMA:INFORMATIVO:

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

CLASE N° 78                                                FECHA: 30 de junio de 2020

TEMA: ENVÍO DEL PORTAFOLIO ESTUDIANTIL

Instrucciones cómo enviar los Portafolios:

1)      Ponga su nombre y curso en todas y cada una de las hojas.

2)      Numere todas las hojas

3)      Tome fotos o escanee (si tiene Scanner)

4)      Incluya las tareas y las pruebas de bloque

Comprimir las imágenes en Zip o también puede

Convertir las imágenes en archivos PDF o también puede,

Elaborar un archivo en Word o en Paint.

Esto facilitará el envío y la descarga de imágenes.

5)      Si envía desde el celular

a)      Clic en compartir

b)      Seleccione Gmail

c)     Para: ocptareas@gmail.com

d)    Asunto: Nombre del estudiante, curso y teléfono👈👀💦

e)      Clic en enviar

6)      Si envía desde el computador cree una carpeta con todos los archivos y envíe.

7)      Usted recibirá un Chat o correo confirmando la recepción

FECHA DE ENVIO: Desde el 01 al 07 de julio de 2020

Si algún estudiante tiene dificultades escriba al correo ocptareas@gmail.com

o envíe un Chat. 0980210744 es un gusto atenderles.

⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶⇶

TRABAJO DE REMEDIAL

Favor enviar al correo electrónico ocptareas@gmail.com👈👀💦

1.       Plantear y resolver un ejercicio estadístico propio (NO COPIADO)

a)       Realizar el conteo de datos.

b)      Elaborar una Tabla de Distribución de Frecuencias

c)       Diseñar un Gráfico Estadístico apropiado. (barras, pastel)

d)      Hallar las Medidas de Tendencia Central

e)      Redactar conclusiones

2.       Hallar la Ecuación de la circunferencia con centro en el punto (h, k) y radio r =

a)       Asignar las coordenadas del punto (h, k) en cualquier cuadrante.

b)      Asignar el valor del radio.

c)       Elaborar el gráfico

y
es